Introduction
Matrix seriation in archaeology consists of chronologically ordering a set of archaeological contexts based on the distribution of different characteristics (artifact types). This process involves finding an arrangement by permuting the rows and/or columns of a contingency table.
The origin of matrix seriation is attributable to the British archaeologist Flinders Petrie (1899), who successfully established an important chronology for ancient Egypt in 1899. Petrie’s formulation of the method was in archaeological terms, devoid of any mathematical formalism. For this, we had to wait until the middle of the 20th century and the work of Brainerd (1951) and Robinson (1951), followed by the contributions of Kendall (1969b, 1969a). Seriation is not unique to archaeology, and some of the crucial advances have been made in other disciplines, notably the work of Bertin (1967) on graphic semiology and the work of Benzécri (1973) on correspondence analysis.
The matrix seriation problem is based on archaeological conditions and statistical assumptions (Dunnell 1970). Theses assumptions create a distributional model and ordering is accomplished by arranging the matrix so that the class distributions approximate the required pattern. The resulting order is inferred to be chronological.
This post briefly illustrates how to perform a correspondence analysis based seriation with kairos, dimensio and tabula.
Getting Started
To start off, you should install the tesselle packages, if you haven’t already:
install.packages("tesselle")Then, you need to load and attach the package:
Now we can use the functions from the tesselle packages.
Case Study
In this post, we will be exploring the zuni dataset from Peeples and Schachner (2012). This dataset contains ceramic counts from the Zuni region of the American Southwest: each observation is an assemblage and each variable is a ceramic type (see help(zuni, package = "folio")).
To get a graphical overview of the data, you can plot a Ford (1962) (battleship curve) diagram:
Correspondence Analysis (CA) is an effective method for the seriation of archaeological assemblages: the order of the rows and columns is given by the coordinates along one dimension of the CA space, assumed to account for temporal variation. Let’s use the seriate_average() function:
seriate_average() returns the full results of the correspondence analysis. You can explore these results:
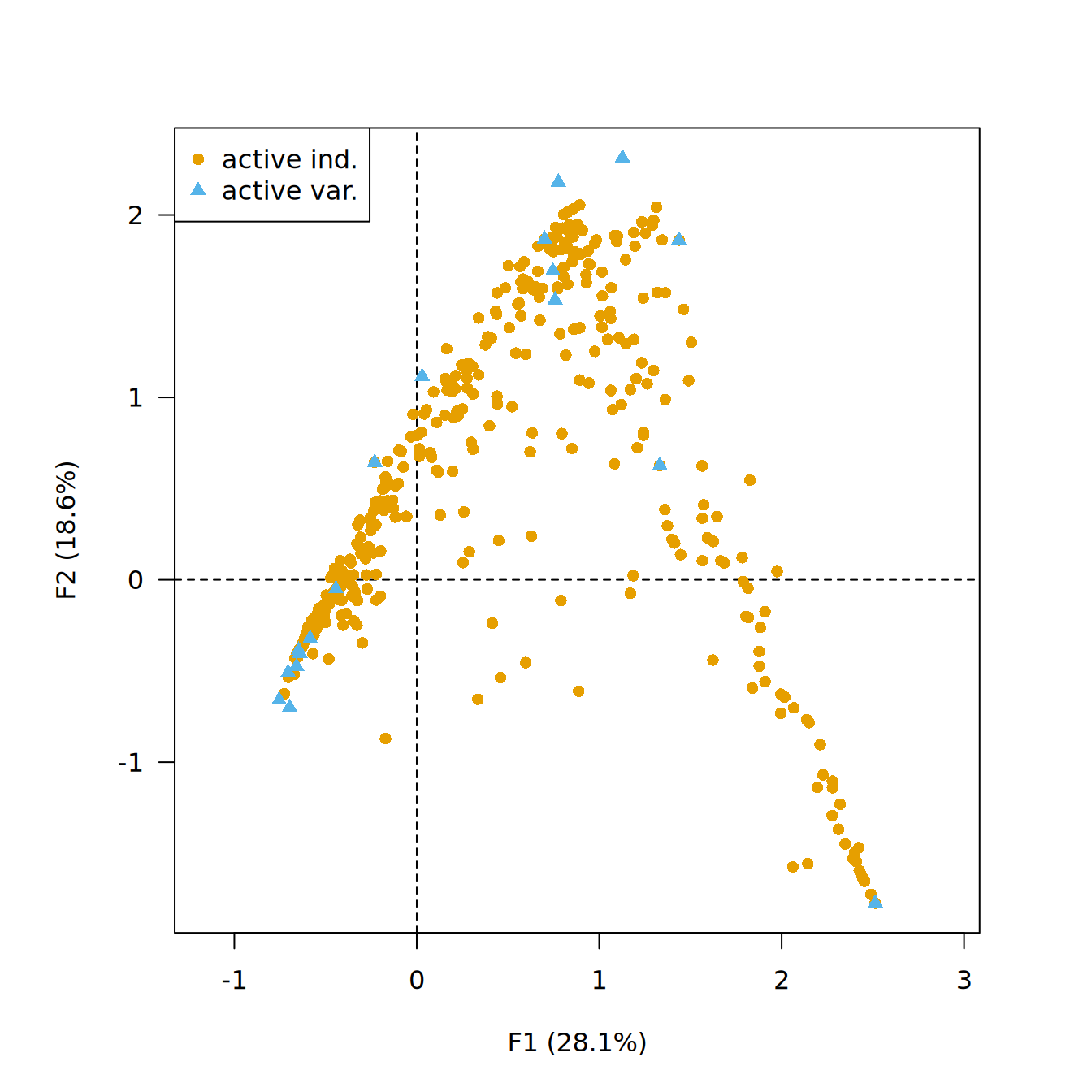
If the results of the correspondence analysis are satisfactory, we can then permute the rows and columns of the original data matrix:
Plot a Ford diagram of the permuted data:
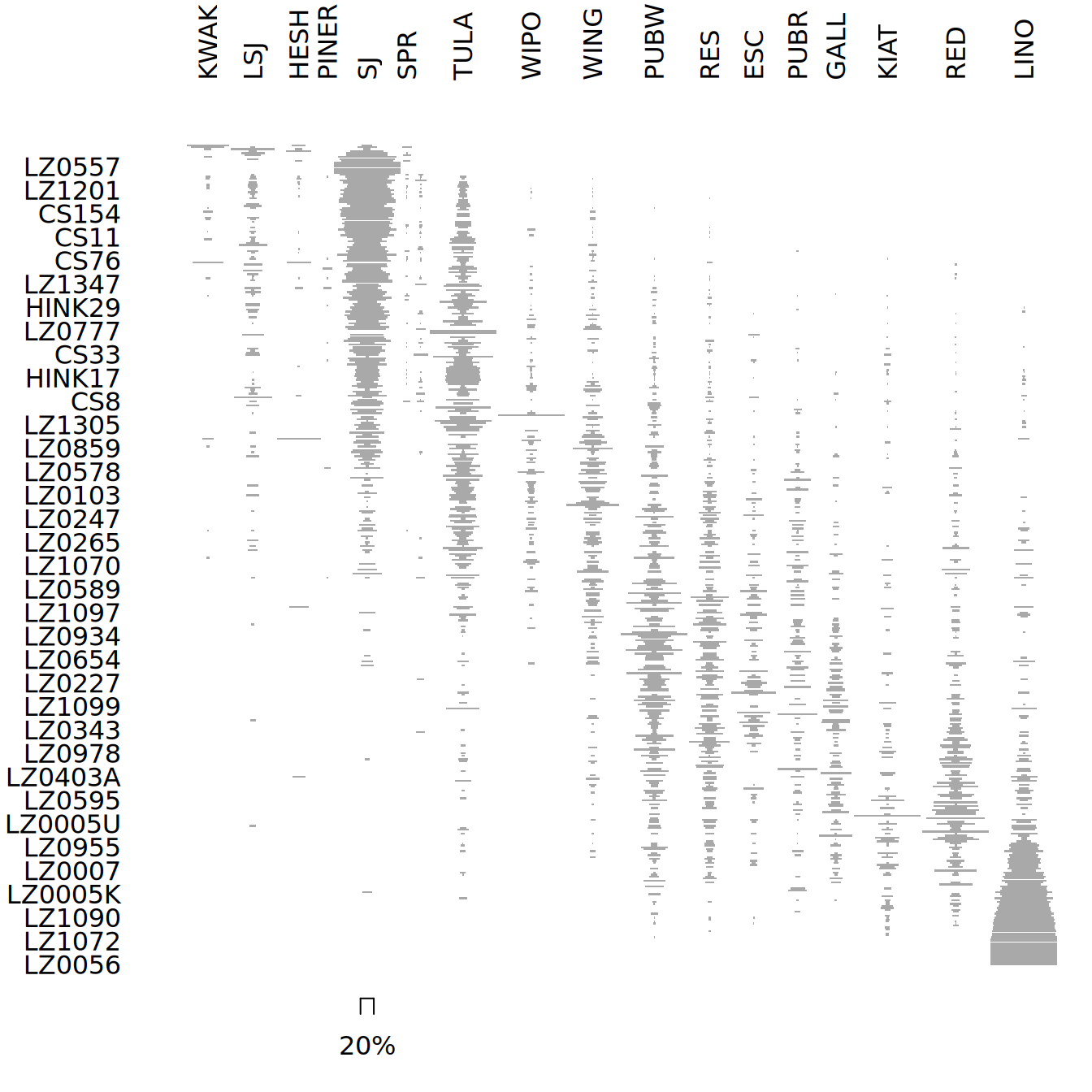
Note that the direction of temporal change within the correspondence analysis space is arbitrary: additional information is needed to determine the actual order in time.
References
Reuse
Citation
@online{frerebeau2023,
author = {Frerebeau, Nicolas},
title = {Archaeological Seriation},
date = {2023-08-22},
url = {https://www.tesselle.org/learn/seriation},
langid = {en}
}